2.3. B-trees
In this lecture we look at...
[Section notes PDF 159Kb]
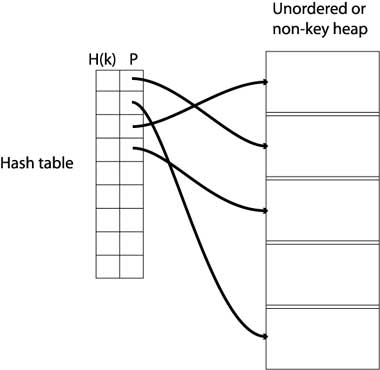
2.3.01. Hash tables
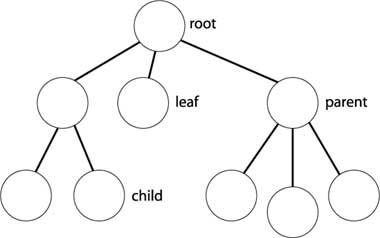
2.3.02. Tree structure
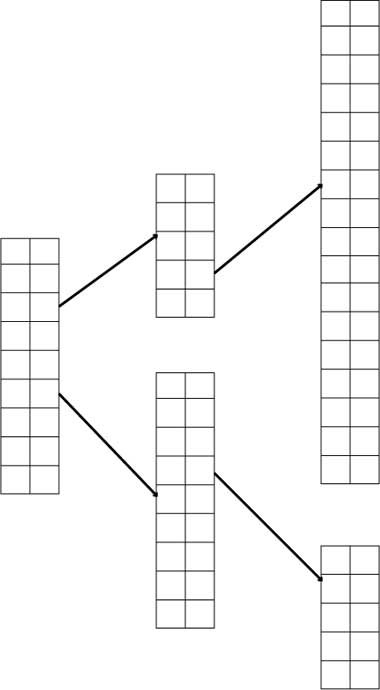
2.3.03. Multi-level indices
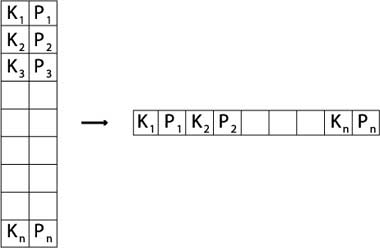
2.3.04. Index zipping
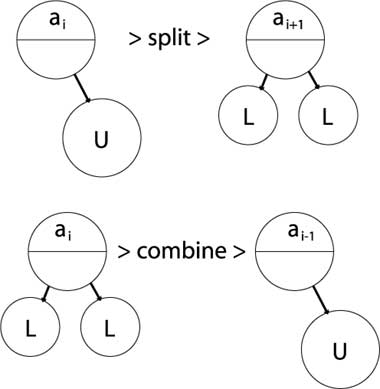
2.3.05. B-tree
2.3.06. B+ trees
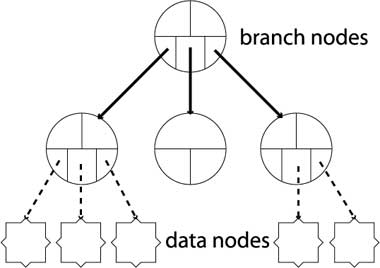
2.3.07. Properties of B+ trees
- Balanced
- All leaf nodes at same level
- Record search takes same time for every record
- Partitioning needs to be comprehensive
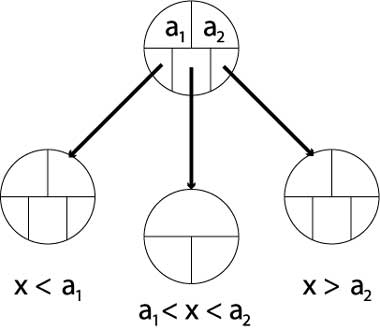
- B-tree: a1 < x < a2
- B+tree: a1 <= x <= a2
- Why?
- because all data for partition values must be in the lowest level of the tree